IMT sent me a note about their name change. I wrote back to ask them to work harder on gravitational imaging sensors which can be adaptations of MEMS accelerometer technologies they are already familiar with.
I am encouraging anyone who makes MEMS accelerometers and inertial sensors to at least try to prepare for gravitational sensor networks. My rather informed guess is that the first ones to address it seriously will lay the foundation for gravitational sensor networks and commodity products. It will be possible to make cell phone gravitational GPS units. It won’t happen over night, but it will probably happen. Whether MEMS or electrochemical, or atom interferometer or some other of the various approaches will get most of that market, I don’t know. I want it to calibrate the weather and climate models. And that fits the needs of every small city and community and location on earth. So “professional” versions of gravitational detector arrays, gravitational imaging array, gravitational scanners, gravitational communications networks – will likely grow quickly once people see that “it is not hard, just tedious”.
Stephen,
I appreciate the announcement. For many years I have been tracking MEMS sensor developments for the Internet Foundation. Particularly what I term “gravitational imaging array” applications.
There are a few MEMS gravimeters now. Liang Cheng Tu in China and the Middlemiss group at University of Glasgow.
Essentially they adapted cell phone MEMS accelerometers to be sensitive enough to track the tidal gravity signal from the sun and moon. To put that in perspective, the superconducting gravimeters (SGs) that are still the gold standard in that type of gravitational monitoring have slightly better sensitivity at 1 sample per second. But the SGs use liquid helium cooling and superconducting levitation and cost closer to a quarter million each, when the China group had talked about putting their in cell phones.
The reason I know this is because about 20 years ago i wanted to measure the speed of gravity. When I went to calibrate the SG network, I found they were not on an absolute standard. So I used the sun and moon tidal signal as a universal reference. Because the SGs are single axis instruments, I could not extend that work. So I went through all the seismometers in the IRIS.edu network to find that the broadband, three axis seismometers – operating as accelerometers – were sensitive enough on all three axes to calibrate to the three orthogonal parts of the sun moon tidal signal. It is the suns acceleration at the station minus the sun on the center of the earth, plus the moons gravitational acceleration on the station minus the moon on the center of the earth. To that vector add the centrifugal acceleration at the station from earth rotation. That vector dot into the station North East Vertical unit vectors to get the three time series for the expected acceleration at the instrument. It only requires a linear regression (an offset and scale factor) to fit the SG and seismometer signals. It is so precise that tiny variations in location and orientation of the device shows up as change in the sum of squares of the residuals.
For permanent stations or faster sampling rates and higher sensitivities, this means that portable devices like MEMS gravimeters, and atom interferometer chip gravimeter, and compact electrochemical gravimeters (there are also Bose Einstein, “quantum”, Mossbauer and other groups working on different technologies for the same thing) – a three axis device will be sensitive enough to use for “gravitational GPS”. To solve for location and orientation of the sensor. And gravity is not affected by ionospheric electron density variations, and gravity can penetrate the earth and ocean. So there are practical consequences.
My interest is to use the gravimeter arrays to calibrate the seismic models of the earth interior. The signals from larger earthquakes are strong enough the gravitational potential changes due to seismic waves – traveling at the speed of light and gravity (they are identical, not just close, but identical) – can be monitored in real time, imaged and tracked. The seismic (acoustic) models are well developed and they can be used as reference signals to get the gravimeter arrays calibrated. Then the gravitational arrays feed back their different gravitational view to the seismic network. It is 3D models and precise timing. The Japan earthquake registered a gravity signal on the SG and the broadband seismometer network – exactly the only instruments capable and running then. That shows the the gravity signal can be used that way.
Jan Harms and others at LIGO spend a lot of time trying to suppress the earth and solar system gravitational “noise”. I keep trying to get them to call it a “gravitational signal” since it has great value for earthquake early warning, calibrating many earth based geophysical and meteorological sensor networks and models. The global climate groups cannot get fine grained 3D and time constraints on their local models, and the raders, lidars, ground sensors, drone and ballon sensors all are gradually getting merged to constrain the local models. But about 5% of the SG signal is atmosphere. To put that in perspective, about 95% of the SG signal is pure Newtonian vector tidal gravity. That is why it makes a good gravitational reference for global coordination and for gravitational GPS applications. The about 4-10% of the signal is meteorological – moisture and rain and convection and wind and density. It is not hard to estimate the signal at the station for any given atmospheric model (or ocean model. The waves and ocean tides and currents also have gravitational signals)
I want it to scan the interiors of the sun, moon, earth and plants and other bodies. And to extend the range of gravitational imaging and application to the same range as electromagnetism – from roughly picoHertz to ZettaHertz. For many practical things gravitational and electromagnetic technologies are identical. They use the same mathematical and computer modeling methods for processing and visualizing and calibrating. The same nano and pico scale sensing, amplification, same types of ADCs, low latency raw data processing, data storage and communications. Same archiving and global sharing, same methods of online collaboration, modeling and teaching and sharing.
At GravityNotes.Org are a lot of notes mostly related to “earthquake early warning” and “elastogravity” (a rather unfortunate name one group called the signals that come from seismic waves (acoustic displacements in the earth) as gravitational signals at the speed of light and gravity to the sensor arrays.
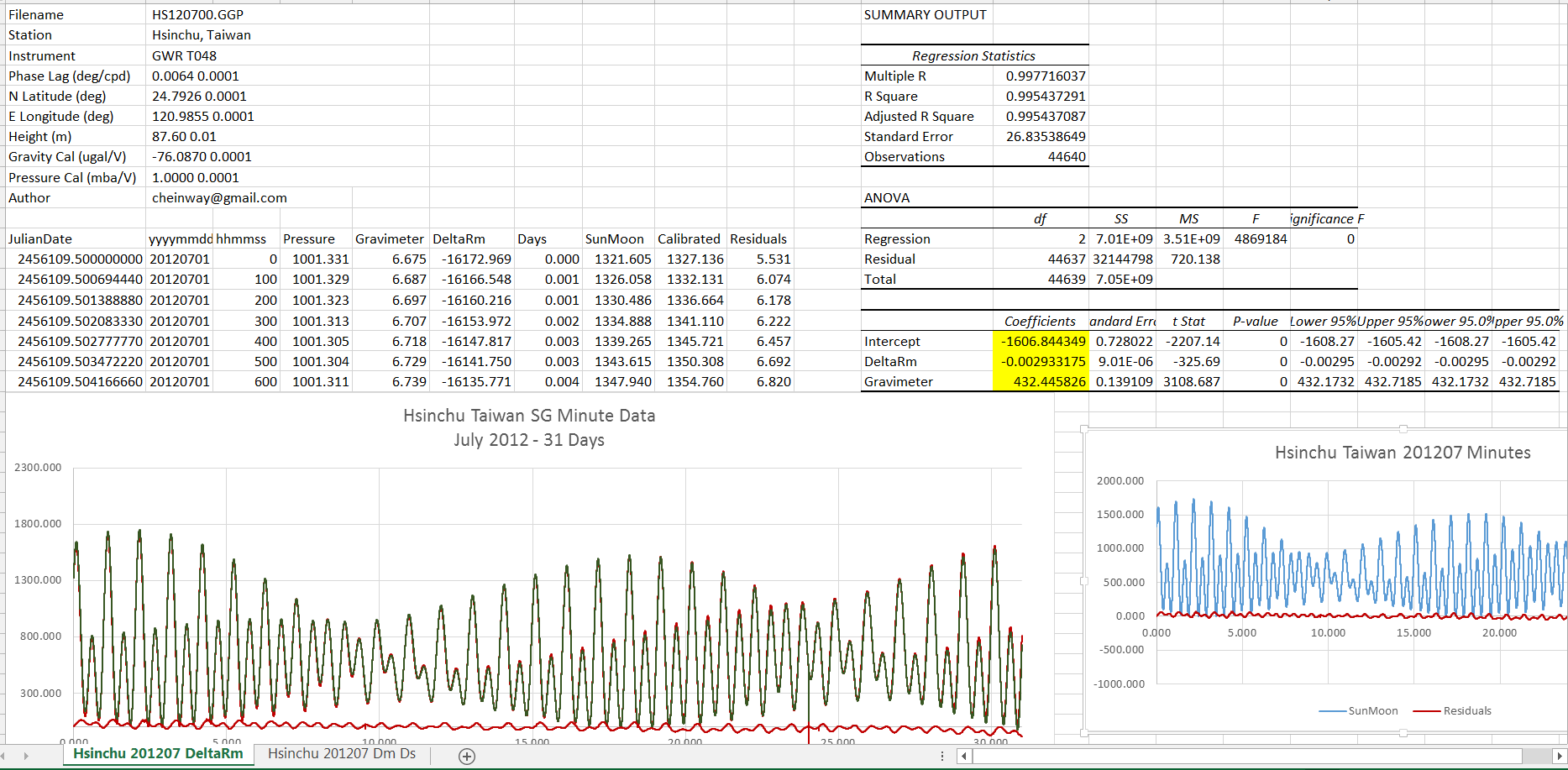
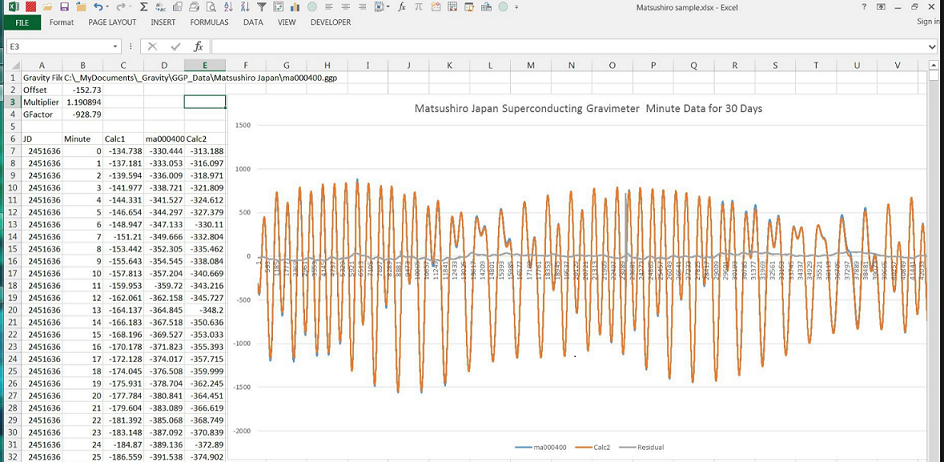
At the top is a link to a spreadsheet that shows what one axis of the sun moon tidal signal looks like at a SG station and how well it fits — with only two numbers – an offset and a scale factor. In the spreadsheet that is cells M17 and M19. I have a tiny correction that is needed for months long studies where I corrected for earth moon barycenter rotation.
You can just see the calculated sun moon reference signal in red underneath the station reading – after they have been scaled to fit this month long dataset. The red residual at the bottom is almost all atmospheric and some ocean and earth tides if you are near the ocean. After you remove the sun moon part the atmosphere gets easier to use. And with clusters of three axis gravimeters easier still. It is a fair amount of data. But the regressions can do done continuously with the processors in cell phone, tablets, desktops. GPS need satellites, transmitters, receivers and constant attention to exact timing. I do not know what technology will win out. I think the atom interferometer methods could be very good, but the groups are slow and expensive. The Bose Einstein have some good methods but all academic. The Mossbauer is actually measuring the changes in the gravitational potential itself. I consider it is measuring a change in the index of refraction of the vacuum induced by the changing gravitational potential – just like LIGO measures the change in the rate of clocks at that location based on the apparent difference is distances.
Richard K Collins, Director, The Internet Foundation